🤖 Machine Learning - Descomplicando o hype!

Fala aí, turma! Tudo bem?

Venho usando o TabNews há um tempinho e gostei muito, muito mesmo da comunidade e da plataforma, mas vejo pouco conteúdo de ML/AI técnico ou bruto, no caso, AI que não sejam agentes de LLM (que sinceramente, leva uns 20 minutos pra desenvolver) ou "Vibe Coding" (...), então pensei em compartilhar um pouco desse universo sensacional que é o machine learning. Hoje quero compartilhar um pouco de conhecimento em uma espécie de introdução a esse mundo cheio de termos estranhos e coisas que o pessoal parece gostar de complicar.

Dados e mais dados

Tenho certeza que você já ouviu falar de rede neural, durante um tempo era só nisso que se falava, em como o computador é capaz de aprender e se adaptar a um conjunto de dados, tipo... como o Google sabe que eu quero comprar um anzol se eu pesquisei por vara de pescar? Como isso se relaciona?

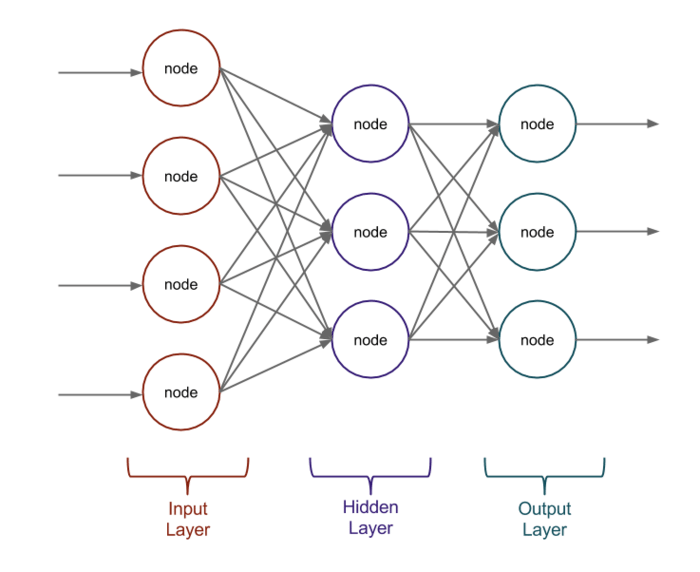
Bom... é aí que mora o X da questão (literalmente): uma rede neural, essa belezinha aí em cima, aprende a relacionar as características de um dataset. Ok... o que isso significa?

Um dataset é literalmente, como o nome diz, um conjunto de dados. Digamos que temos um site de streaming e a gente precisa recomendar filmes que o usuário vai gostar, nesse caso, teríamos um dataset assim:

# meu_dataset_de_usuarios_favoritos_s2.csv
user_id,movie_id,rating
0,1034,5.0
0,1255,3.5
1,1034,4.5
...

Nesse exemplo, temos usuários, filmes e uma classificação que vai ser a nossa característica principal, no campo de ML, chamamos isso de feature e o processo de entender essas features e como se relacionam de Feature Engineering.

Quanto mais dados, melhor!

Computadores sonham com ovelhas elétricas?

Muito legal essa coisa toda de dataset e features e sei lá o que, mas... como uma rede neural REALMENTE aprende?

Agora que você já sabe como os dados aparecem no Machine Learning, vamo começar do começo com uma rede neural super, super simples que começou a ser usada lá na década de 60 e vamo entender ela do zero.

Esse negócio estranho aí em cima é um Modelo de Regressão Logística. Cada "nível" de bolinhas é um layer/camada da rede neural, cada um tem seu papel e faz uma alteração nos dados originais. Vamo quebrar ele em partes:

Primeiro layer

A primeira camada é onde os dados são ingeridos. No nosso exercício mental, a gente vai usar um dataset super, super clássico na área: MNIST, um conjunto de imagens de números escritos à mão e vamo usar esse rede neural pra aprender a identificar esses números. Nesse caso, a primeira camada vai receber eles. Dá uma olhadinha em como ele se parece:

Ué... mas no primeiro exemplo era um CSV, como é que vou ingerir uma imagem na rede neural?

É aí que entra um dos pontos mais importantes e fundamentais do Machine Learning: todos os dados ingeridos devem ser numéricos. Você deve ter notado que no primeiro exemplo, tudo ali era número, podia ser justificado pelo fato de serem IDs e uma classificação numérica do filme, mas isso é proposital!

Toda rede neural vai aprender o relacionamento das características de um conjunto de dados por meio de métodos matemáticos, é por isso que tudo precisa ser número.

Certo, e como aplicar isso em imagens?

Bom, é mais simples do que parece: basicamente, "pixelizamos" a imagem, isso é, transformamos ela em uma matriz de valores, onde cada componente da matriz é um número que define a intensidade da cor branca no pixel específico:

As imagens vão ser inseridas dessa forma na rede neural.

Na primeira camada a gente consegue ver várias bolinhas, cada uma delas (matematicamente representadas por X_{iM}) é uma imagem pixelizada, ou seja, uma matriz de valores númericos.

Nesse exemplo, a rede neural vai ser capaz de identificar se um número é um 0 ou 1. Mas como?

Segundo layer

Na segunda camada, é onde a mágica realmente vai acontecer. Ali acontece uma operação matemática conhecida como Regressão Logística, ela é capaz de criar um filtro com base nas features/características dos dados ingeridos, que vai definir se a imagem enviada no "prompt" da rede neural é um 0 ou um 1, logo isso vai ser explicado, primeiro, vamo dar uma olhada na função matemática:

Pra criar um relacionamento entre todas as características do dataset, a gente precisa tornar eles um só e buscar coisas em comum. Por exemplo: os pixels brancos das imagens do número um parecem sempre ficar numa certa região da imagem, dá pra tirar um filtro daí, como na imagem abaixo:

Isso funciona pro 0 também. O 1 vai ser o nosso resultado positivo e o 0, o negativo, então a rede neural vai dar N pontos positivos pra cada pixel na imagem do "prompt" que estiver na região que ela aprende que o número 1 costuma ocupar, e N pontos negativos pra cada pixel que ocupar as regiões do número 0. Assim, temos um Sistema de Classificação Binário. O filtro acima é como a rede neural pensa.

Matematicamente isso pode ser visto aqui:

Onde:

b_0 é o bias da rede neural, uma constante que mantém os dados estáveis;

X_{iM} é a imagem pixelizada;

b_M é o parâmetro que vai ser ajustado na rede neural, isso aqui define o filtro que vimos acima.

O símbolo \bigodot basicamente define que a seguinte operação vai ser realizada:

Ou seja, para M parâmetros da rede neural, X_{iM} vai ser multiplicado pelo parâmetro b_M, basicamente, um relacionamento é criado aqui!

Cada parâmetro em uma rede neural começa com um valor aleatório e é ajustado conforme as epochs/gerações passam no treinamento do modelo, isso significa que a rede neural está aprendendo! No fim, vamos ter aquele filtro que foi gerado com base no ajuste dos parâmetros M.

Ufa... a parte mais chatinha da matemática passou!

Depois de tudo isso, o que a rede neural realmente vai retornar pra gente?

Terceiro layer

A terceira camada dessa rede neural é o passo final de tudo e vai determinar oque vai ser retornado. No caso específico desse modelo, ocorre o último processo matemático onde uma Função Sigmoid é executada nos dados gerados pela segunda camada. É... o que isso significa?

A Função Sigmoid transforma valores gerados por uma rede neural em porcentagens, isso é, dados probabilísticos, isso faz sentido por que precisamos saber "quantos por cento" dessa imagem correspondem ao número 1. O retorno sempre vai ser assim: 0.95, 0.01, 0.2, etc.

Isso indica a taxa de correspondência com o número 1, por isso, imagens próximas ao número um recebem valores positivos e imagems do número 0, números negativos. É tudo matemática!

A última operação matemática é super simples e é basicamente isso aqui:

Onde p é a porcentagem de correspondência com o número 1, \sigma é a Função Sigmoid e z_i é o retorno da Regressão Logística.

Pronto, temos uma rede neural! Agora é só colocar qualquer imagem do MNIST nunca vista antes pelo modelo de um número 0 ou 1 e ver o resultado.

Um olhar mais profundo na Regressão Logística

Por que só podemos ver se o número é 0 ou 1? Por que não identificar se ele é 0, 1, 2, 3...

Por ser um exemplo simples, baseado em Regressão Logística, só podemos fazer testes binários com o dataset, isso se dá pela natureza dessa operação matemática:

O gráfico acima mostra uma visualização do que o modelo interpreta com o resultado da regressão logística, onde X_1 são as imagens do número 1 e X_2 são as imagens do número 0. Ele basicamente organiza o dataset em duas classes com base nas características da imagem. Além de só possuir a capacidade de identificar 2 classes, é um modelo linear, ou seja, com capacidade para características simples. Para números complexos, como por exemplo o número 4, que pode ser escrito de diversas formas:

O filtro fica um pouco mais complexo e aí precisamos elevar o nível para um Multilayer Perceptron, onde a operação de Regressão Logística é repetida diversas vezes para obter o relacionamento complexo das características da imagem, podendo suportar variantes de um mesmo padrão! É quase um clustering, mas não é!

Isso é um gráfico de visualização de um filtro de um Multilayer Perceptron:

E isso é um Multilayer Perceptron:

Sim! Computadores sonham com ovelhas elétricas!

Bom, por mais que tenha sido muita coisa pra ingerir provavelmente, foi o melhor que consegui fazer pra "resumir" oque aprendi nos últimos anos em uma introdução a esse universo maravilhoso do Machine Learning.

Peço desculpas se ficou muito longo, complexo, ou não consegui explicar bem alguma coisa. Inclusive, se alguém tiver alguma correção, por favor, não hesite em comentar, estamos sempre aprendendo (e os computadores também).

Sei que o público aqui é mais do web, e por isso acho que é legal ter contato com outras áreas também, principalmente nos tempos em que vivemos que essa área tem crescido tanto.

Muito obrigado por ler até aqui e continue aprendendo!