Por que a matemática é essencial para a programação?
Programar tem muito mais a ver com matemática do que você pensa. Sem saber nada de matemática é impossível trabalhar, não digo sobre resolver equações, calcular logarítmos e afins, mas a interdisciplinaridade da matemática (nome bonito XD) nos ajuda em vários campos da vida.
Com a matemática aprendemos lógica, que é a base fundamental para algorítmos e por sua vez para a programação. Um programador que não sabe lógica não passa de uma máquina de escrever código adoidado, sem nenhum critério. Mas o que isso tem a ver com a matemática em si?
Não existe magia
Tudo o que é construído dentro da programação tem um grande background matemático. Mas não se desespere, hoje em dia temos tudo tão abstraído e prontinho para usar que praticamente ninguém precisa lidar com problemas matemáticos diretamente ao programar caso não seja necessário.
Mas por que é importante entender esses conceitos matemáticos por trás da programação?
Nos últimos tempos vemos uma grande popularização da programação e das profissões adjascentes, todos querem uma oportunidade de emprego na área que mais cresce no mercado. Isso faz com que existam muitos iniciantes na área, aprendendo para logo se tornarem programadores e consequêntemente uma ampla concorrência para vagas de estágio e de júnior.
Essa concorrência faz com que o candidato precise se destacar de alguma forma. Mas veja, conhecer tudo o que tem de baixo do capô do carro não te fará um bom motorista, mas te fará conhecer os limites e um leque de outras possibilidades que aquelas peças podem proporcionar. Da mesma forma, nós programadores trabalhamos com limites e possibilidades a partir das nossas ferramentas, que são as linguagens de programação, conhecer o que há de baixo do capô pode até não nos fazer programadores melhores, mas nos fará entender melhor determinados comportamentos. Uma forma de se destacar é aprender esses conceitos de baixo do capô e isso sempre irá passar por uma base matemática muito sólida.
O estudo aliado à prática é imbatível quando queremos melhorar e nos destacar em um ambiente de ampla disputa, certamente aquele programador que entende algumas questões de baixo nível poderá se destacar muito por entender alguns comportamentos e conceitos oriundos da linguagem que utiliza. É aí que a matemática entra, ela é uma ferramenta para que possamos resolver problemas e entender conceitos de baixo e alto nível.
Para exemplificar isso, vamos resolver um problema muito conhecido da matemática e programação, para entendermos como isso funciona, o cálculo da função Seno(x), que mistura tópicos básicos e avançados de matemática.
Como calculamos seno(x)?
Ao passarmos pelo ensino médio, aprendemos que para calcular o seno de um ângulo α precisamos de um triângulo retângulo e seno(α) = CO / HIP, onde CO é o cateto oposto ao ângulo e HIP é o lado maior do triângulo.
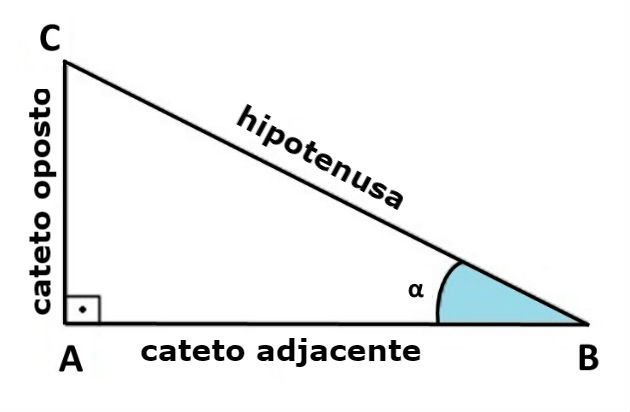
O que precisamos entender é que a função seno não é simplesmente calculada de uma forma direta, como uma função f(x) = x², ela é um pouco mais complexa.
Para entendermos isso, tudo parte de um conceito: sequências
1, 2, 4, 9, 16, ..., n²
Uma sequência, segundo a matemática nada mais é que... bom, uma sequência. As sequêncieas têm algumas propriedades:
-
Ordem fixa
Os elementos de uma sequência tem uma ordem pré definida, não podemos sair os trocando de ordem, pois teríamos uma nova sequência. Por exemplo:
{a} = 1, 2, 3, 4, 5 é uma sequência simples, que tem apenas 5 elementos que seguem a ordem dos números naturais entre 1 e 5 inclusive. Mas e se invertermos as posições de 3 e 5?
{b} = 1, 2, 5, 4, 3 agora é uma nova sequência com outra lógica. -
Segue uma regra pré definida
Todos os elementos seguem uma lógica para estarem ali, o que é meio óbvio, mas precisa ser documentado. Por exemplo, a sequência {m} = 1, 2, 4, 9, 16 segue a regra mi = i².
Caso um conjunto de números não tenha uma regra então não pode ser uma sequência. Essa regra é chamada lei de ocorrência de sequência e é uma condição de existência. -
Termo geral
A forma com que vimos a regra da sequência {m} é um termo geral de sequência, isso é, sabendo o índice i, podemos saber qual é o elemento da sequência relacionado com esse i, por exemplo:
{a} = 3, 6, 9, 12, 13, ..., 3n
A sequência {a} tem um termo geral 3n, pois a sua regra é que cada termo é um múltiplo de 3, podemos saber quando vale qualquer elemento da sequência a partir de seu índice n. Podemos também utilizar o termo geral como notação para representar a sequência.
-
Pode ser finita ou infinita
-
Sequências infinitas podem convergir ou divergir
Isto é, o termo geral quando o índice da sequência tende a infinito converge para uma constante, caso contrário a sequência diverge. Por exemplo:
{b} = 1/n
Para sabermos se a sequência converge ou não basta tirarmos o seu limite quando o seu índice tende ao infinito:
lim n→∞ 1/n = 0, ou seja, quando n tende ao infinito o termo geral b tende a 0 o que significa que a sequência converge.
Mas e se somarmos isso tudo?
Certa vez um matemático qualquer teve uma brilhante ideia:
E se eu somar todos os termos de uma sequência?
A partir dessa ideia surgiu o pesadelo de muitos e a alegria de outros: as séries. Uma série nada mais é que a soma de todos os elementos de uma sequencia infinita. Ou seja, para uma sequência {a} = n + 1 existe uma série 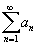
Da mesma forma que com as sequências, séries podem convergir e divergir. Esse é assunto para várias semanas em um curso de Cálculo B e Análise Matemática A, então não vamos nos aprofundar muito, o que importa saber é que uma sequência que diverge é praticamente inútil, portanto sempre estamos preocupados com a convegência das séries.
Algumas séries tem o que chamamos de intervalo de convergência. Isso ocorre quando uma série tem um termo geral que depende de outra variável, como por exemplo:
P(x) = an(x - c)n (entenda implicitamente que a função P(x) é uma soma infinita).
No caso de P(x) a série não depende apenas de n, ela depende também do valor de x, que é uma outra variável. Enquanto |x| < c a série converge e, para qualquer outro valor, ela diverge.
Resolvendo o problema do seno(x)
Agora as coisas vão complicar um pouco, pois usaremos o conceito de derivada, que é um conceito simples de cálculo A mas avançado na matemática. Sugiro que pesquise bastante para entender o conceito e a seguinte solução.
No estudo de séries conhecemos a Série de Taylor que é uma das séries mais importantes. A partir dela podemos aproximar o valor de várias funções, como logarítimos, exponenciais e o próprio seno. Ela é escrita da seguinte forma:

Veja ela tem um determinado intervalo de convergência, isso é muito importante. O valor de an é a n-ésima derivada da função que se quer aproximar. Dessa forma, podemos representar a série de Taylor de outra forma, que chamamos de polinômio de Taylor:

Veja que f'(c) é a derivada de f(c), f''(c) é a segunda derivada de f(c) e assim por diante. A derivada é feita em relação a n, não a x, por isso os termos que se sucederam, não vamos entrar em detalhes pois é um assunto bem extenso. O termo c é uma constante, que normalmente é um valor aproximado ao que queremos calcular, por exemplo:
Para a função ln(x), caso quisermos saber quanto vale ln(2,1) podemos aproximar 2,1 para 2, pois esperamos que o valor de ln(2,1) seja próximo de ln(2), assim:

Substituindo x pelo valor 2,1:

Note que para esse exemplo utilizamos apenas três termos da série de taylor, mas quanto mais termos utilizamos, mais próximo o valor da série se aproxima do valor real.
De Taylor para Maclaurin
Na série de Taylor temos um caso especial, que é a série de Maclourin:

Na série de Maclaurin aproximamos a série de Taylor em torno de c = 0. Com essa série podemos calcular o valor aproximados de várias funções, como as trigonométricas e exponencial.
A função que queremos calcular é f(x) = seno(x), então vamos derivar!
f'(x) = cosseno(x)
f''(x) = -seno(x)
f'''(x) = -cosseno(x)
f''''(x) = seno(x)
e daqui por diante tudo se repete. A grande vantagem é: como estamos nos aproximando de 0, temos um valor conhecido tanto para seno(0) quanto para cosseno(0).
seno(0) = 0
cosseno(0) = 1.
dessa forma:

Solução no código
Vamos colocar isso agora no código, vou fazer a solução em javascript para ter um fácil entendimento, fique a vontade de resolver em outras linguagens e publicar aqui também :).
function seno(x) {
function fat(n, total=1) {
if(n === 1) return total
else {
return n * fat(n - 1, total * n)
}
}
return x - ((x ** 3) / fat(3)) + ((x ** 5) / fat(5)) - ((x ** 7) / fat(7))
}
Pronto! Acabamos de escrever uma função que calcula qualquer valor de seno entre -π/2 e π/2 (sim, a função não irá funcionar para qualquer valor real da forma que está).
Coisas que deixamos de lado
Faltaram algumas coisas importantes para essa solução:
-
A função funcionar para qualquer valor real, assim como a função de cada linguagem
Atualmente a função apenas funciona para |x| < π / 2, o que torna a função não muito utilizável. -
Melhorar a precisão
Se você implementar e rodar a função verá que o valor retornado é diferente do que a função Math.sin() retorna, em algumas casas decimais. Saiba que é possível ajustar a precisão para que fique exatamente igual, pois esse é o método que a maioria das linguagens utiliza para implementar a função seno, é importante termos uma boa precisão da nossa função.
Em uma próxima postagem irei resolver esses problemas e falar um pouco sobre precisão matemática na computação.
Considerações finais
Como puderam ver, para construirmos uma função muito simples que calcula um seno de um determinado ângulo precisamos passar por vários conceitos, desde sequências até cálculo e séries, isso nos mostra um fator básico da matemática e isso também vale para a programação. Nada do que aprendemos na programação é inútil, na pior das hipóteses vai nos ajudar a resolver problemas bem específicos. Da mesma forma, caso pulássemos a etapa de sequências por exemplo, jamais saberíamos o que são séries e não teríamos solução para o nosso problema, pular etapas na programação e na matemática é fatal para a nossa evolução.
Podemos até concordar que saber implementar uma função seno é inútil, pois já temos uma ferramenta para isso em todas as linguages, mas temos que lembrar que isso é uma base que no futuro irá nos ajudar a resolver novos problemas.
Lembre-se, a essencia da programação é a matemática, aprender sobre seus conceitos te fará um programador melhor e irá impactar diretamente nos seus códigos.
fonte das imagens: Engenharia 360