Entendendo de vez o PathFinding A*

Estudar e tentar entender algoritmos de programação é sempre um desafio e tanto. Nos últimos dias resolvi desenvolver um jogo em HTML 5 e typescript. Mas aí você deve estar se perguntando: "Por que raios alguém teria motivação de escrever um jogo do zero?"

A resposta é simples: adquirir conhecimento e resolver desafios.

Sim! O processo de criação de um jogo envolve vários desafios e problemas, que precisam ser resolvidos usando lógica de programação e organização.

Como servidor estou usando o NodeJS e MySQL de banco de dados. A conexão entre cliente e servidor é feita através do Websocket nativo do Javascript e vem funcionando muito bem para fins didáticos.

Enquanto escrevia este jogo, me deparei com o seguinte problema: imagine que você precisa calcular o menor caminho do ponto A para o ponto B, desviando de colisões e objetos no mapa… Ficou difícil de imaginar? Tudo bem.. Desenhar é sempre mais fácil.

Considere o seguinte mapa abaixo.

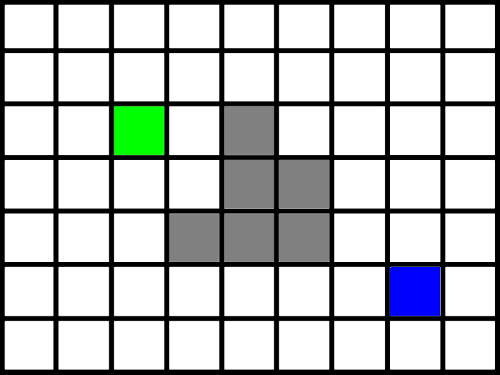
Agora imagine que queremos chegar do quadrado verde até o quadrado azul, pulando de nó em nó (é assim que vamos chamar cada 'célula' do mapa). Imagine também que os nós na cor cinza são obstáculos, a qual devemos evitar, ou seja, só podemos andar em quadrados da cor branca.

Uma das formas de calcular esse caminho é usando um algoritmo chamado A* (ou A Estrela, no bom e velho pt-BR).

Para entender como esse algoritmo funciona, vamos simplificar nosso mapa, usando como exemplo o mapa abaixo.

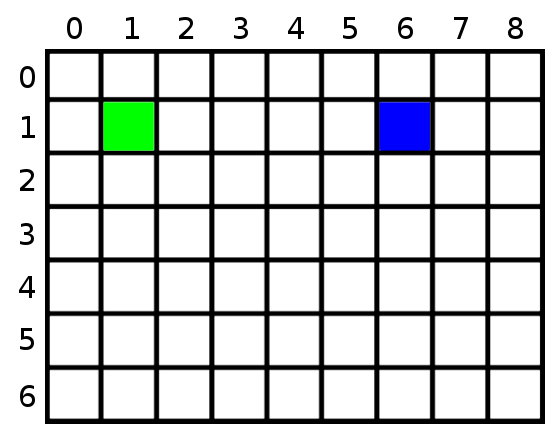
Tomando por base as coordenadas X, indo de 0 à 8 e Y de 0 à 6, podemos afirmar que o nó verde (ponto de partida) está na posição x = 1 e y = 1, e que o nó azul (destino) está na posição x = 6 e y = 1.

Com essas informações, já podemos começar a entender como o algoritmo funciona, então vamos nessa…

Entendendo o algoritmo

A melhor forma de entender o algoritmo é separa-lo por partes.
Imagine que você está no nó de partida (1,1) e você quer ir para o nó de destino (6,1).

O primeiro passo é considerar o nó de partida (1,1) como nó atual.

Tendo esse nó como base, devemos então pegar todas as opções de nós que você pode ir, a partir dali. Para facilitar, vamos ignorar caminhos diagonais. Sendo assim, temos como possibilidades o nó de cima (1,0), o nó da direita (2,1), o nó debaixo (1,2) e o nó da esquerda (0,1) conforme vemos na cor verde clara na imagem abaixo.

Mapa com os nós mais próximos do nó de início destacados em verde claro.

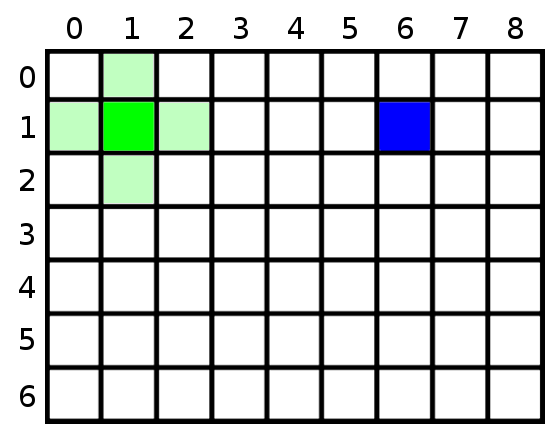
Agora, como saber para qual nó devemos ir, vamos entender alguns conceitos desse algoritmo.

Cada nó carrega consigo algumas informações. São elas:

• Custo
• G
• H
• F
• Parent
• Posição

Vamos um por um…

Custo:
O custo é o preço a ser pago para que a gente possa ir de um nó para outro.

Por exemplo, imagine que estamos na cidade A, e num fim de semana queremos visitar uma outra cidade, para conhecer… ao olhar o mapa eu vejo que todas as cidades que estão na direção ortogonal (em cima, na direita, embaixo ou na esquerda) da minha cidade estão a 10 km de distância.

Ou seja, o custo para ir para alguma cidade na ortogonal é de 10 km. De forma semelhante, imagine também que, para ir para uma cidade que fica na posição diagonal, com relação a nossa cidade A, a distância seja de 14 km.

Então o custo para estas cidades na diagonal seria de 14 km.

G:
O g é a somatória de todos os custos até o momento.

Para entender melhor, vamos supor que decidimos ir para a cidade de cima, que tem custo igual a 10.

Então o G do nó de cima do nosso, cidade a qual estamos indo, será 0 (custo do nó atual) + 10 (custo do nó destino).
G = 10.

H:
É a estimativa do quanto ainda falta para chegar, a partir da cidade vizinha, até a cidade destino (que no nosso caso é o nó azul).

Novamente vamos usar a cidade de cima como referência.
A cidade de cima da nossa está na coordenada 1,0 (em x,y).
Para chegar na cidade azul, temos que andar até 6,1.

Então se subtrair 6 (x da cidade destino) de 1 (x da cidade do norte), e somar com 1 (y da cidade destino)- 0 (y da cidade destino) temos que H será igual a 6.

Veja na formula abaixo para ficar mais fácil:

H = Math.abs(destino.x - norte.x) + Math.abs(destino.y - norte.y);
H = Math.abs(6 – 1) + Math.abs(1 – 0)
H = 6

F:
Aqui apenas somamos o G + H, ou seja, o custo agregado que é o quanto já andamos + a estimativa do quanto ainda falta andar.

No caso do nó de cima temos:

F = G + H
F = 10 + 6
F = 16

Posição:
Aqui apenas armazenamos a posição do nó.
No caso do nó de cima é x = 1, y = 0;

Parent:
Por fim, no parent armazenamos o nó que foi a origem para o nó em questão.

Então, se a gente for da nossa cidade para a cidade de cima, temos como parent da cidade de cima a nossa cidade.

Melhor dizendo, se estamos indo de A para B, então A é parent de B. Se for de B para C, então o parent de C é B, que por sua vez tem A como parent, ficando A -> B -> C.

Pronto...

Tendo essas informações em mãos, devemos então adicionar esses nós (as cidades a qual podemos ir) em uma lista, que chamamos de lista aberta.

Essa lista contém os nós que podemos ir a partir do nó atual.

Em seguida ordenamos a lista de acordo com o F de cada nó, assim o nó que tem o menor F ficará na posição 0 da lista, e o nó com o maior F ficará em último na lista.

Com a lista ordenada em mãos, agora sim podemos saber qual o nó que custa menos para podermos ir. Este será o nó na posição zero.

Retiramos esse nó da lista aberta a adicionamos em uma outra lista chamada lista fechada.

Esta lista conterá todos os nós que já passamos. Essa lista serve para saber quais nós já passamos.

Ou seja, se estamos no nó inicial (1,1) então esse nó está na lista fechada. Se a gente passar do nó inicial (1,1) para o nó de cima (1,0) então o nó inicial (1,1) e o nó de cima (1,0) estarão na lista de nós fechados.

Assim sabemos que não podemos mais ir do nó de cima (1,0) de volta para o nó inicial (1,1).

Esse processo se repete até que o nó atual seja igual ao nó destino, e então sabemos o caminho até o destino.

Implementando o código

Vamos implementar o código, parte por parte, conforme dito anteriormente.

Ps.: Você pode encontrar o código completo (html, javascript, css) no JSFiddle do link: https://jsfiddle.net/renatonolo/o1fvb9wn/

//Adicionando o evento onclick no botão, para chamar a função calcular
document.getElementById("btnCalcular").onclick = calcular;

//Função calcular()
//Pega os valores dos campos de texto da tela e cria a instância da 
//Classe principal "AStar". Essa classe é instanciada e em seguida chamamos a função getPath, que é quem calcula o caminho.
function calcular() {
  let txtConsole = document.getElementById("txtConsole");
  txtConsole.innerHTML = "Calculando...";

  let _x1 = document.getElementById("x1") as HTMLInputElement;
  let x1 = parseInt(_x1.value);
  let _y1 = document.getElementById("y1") as HTMLInputElement;
  let y1 = parseInt(_y1.value);
  let _x2 = document.getElementById("x2") as HTMLInputElement;
  let x2 = parseInt(_x2.value);
  let _y2 = document.getElementById("y2") as HTMLInputElement;
  let y2 = parseInt(_y2.value);

  let n1 = new Node(new Position(x1, y1), 10, 0, 0, 0, null);
  let n2 = new Node(new Position(x2, y2), 10, 0, 0, 0, null);

  let aStar = new AStar();
  let path = aStar.getPath(n1, n2);

  txtConsole.innerHTML = "";
  for (let i = 0; i < path.length; i++) {
    txtConsole.innerHTML += "Passo " + i + ": x = " + path[i].position.x + ", y = " + path[i].position.y + "<br/>";
  }
}

/**** Classe Position ****/
// Classe auxiliar, que armazena a posição de um determinado nó */
class Position {
  x: number;
  y: number;

  constructor(x: number, y: number) {
    this.x = x;
    this.y = y;
  }
}

/**** Classe Node ****/
// Classe auxiliar que representa um nó */
class Node {
  //Posição do nó
  public position: Position;
  
  //Custo para ir para aquele nó
  public cost: number;
  
  //Custo agregado desde o início do caminho até o nó em questão
  public g: number;
  
  //Valor estimado para chegar ao nó destino
  public h: number;
  
  //Somatória do quanto já andamos e o quanto falta andar (G + H)
  public f: number;
  
  //Nó pai do nó atual. Se este nó é o B e viemos de A então A é parent de B.
  public parentNode: Node;

  constructor(position: Position, cost: number, g: number, h: number, f: number, parentNode: Node) {
    this.position = position;
    this.cost = cost;
    this.g = g;
    this.h = h;
    this.f = f;
    this.parentNode = parentNode;
  }
}

/**** Classe AStar ****/
// Classe principal, responsável pela implementação do algoritmo */
class AStar {
  //Lista aberta de nós
  private openNodes: Node[] = [];
  
  //Lista fechada de nós
  private closeNodes: Node[] = [];

  //Método responsável por calcular o caminho partindo do nó inicial (firstNode) e chegando no nó final (lastNode)
  public getPath(firstNode: Node, lastNode: Node): Node[] {
    //A primeira coisa a se fazer é verificar se o nó de inicio é igual ao nó final. Se for, então não precisamos calcular nada, retornamos apenas null.
    if (firstNode.position.x == lastNode.position.x && firstNode.position.y == lastNode.position.y) {
      console.log("First and last are has the same position...");
      return null;
    }

    //Criamos a váriável que armazenará o nó em questão, ou seja, o atual.
    let currentNode: Node = null;
    
    //Adicionamos o firstNode na lista de nós abertos, pois iniciamos com ele.
    this.openNodes.push(firstNode);

    //Enquanto a lista de nós abertos contiver elementos, então é porque ainda estamos procurando um caminho para o destino.
    while (this.openNodes.length > 0) {
      //Pega o primeiro nó da lista de nós abertos, ou seja, aquele que tem o menor valor de F, e consideramos como nó atual, removendo ele da lista de nós abertos.
      currentNode = this.openNodes.shift();
      
      //Adicionamos o nó atual na lista de nós fechados, pois estamos usando ele como parte do caminho para o nó destino.
      this.closeNodes.push(currentNode);
      
      //Limpamos a lista de nós abertos, para não ficar ocupando espaço 'a toa' na memória.
      this.openNodes = [];

      //Aqui verificamos se o nó atual é igual ao nó destino. Se for verdadeiro, então significa que encontramos o caminho para o nó destino. Podemos sair do while...
      if (currentNode.position.x == lastNode.position.x && currentNode.position.y == lastNode.position.y) {
        console.log("Path founded...");
        break;
      }

      //Chama a função que pega todos os nós mais próximos do nó atual e armazenamos na variável aroundNodes. Estes serão os nós de cima, da direita, debaixo e da esquerda, pois não estamos considerando nós na diagonal.
      let aroundNodes = this.getAroundNodes(currentNode);

      //Começamos a calcular os valores referentes aos nós mais próximos. Calculamos G, H, F e dizemos que o pai dele é o nó atual (currentNode).
      for (let i = 0; i < aroundNodes.length; i++) {
        let testNode = aroundNodes[i];
        let g, h, f = 0;

        //Antes de mais nada, precisamos verificar se esse nó que estamos calculando está ou não na lista de nós fechados. Fazemos isto pois não podemos ir de volta para um nó que já foi para a lista de nós fechados. Então, caso o nó que estamos calculando já esteja na lista de fechados, devemos pular para a próxima opção de nó.
        if (this.inCloseNodesList(testNode)) continue;

        //Calcula o valor de G. Este será o g do nó pai (valor que já foi pago para percorrer até o nó atual 'currentNode') + o custo do nó em questão 'testNode'.
        testNode.g = currentNode.g + testNode.cost;
        
        //Descobrimos o quanto ainda falta percorrer do nó em questão 'testNode' até o destino.
        testNode.h = this.heuristic(testNode, lastNode);
        
        //Somamos o quanto já pagaremos, caso escolhesse-mos este nó + o quanto ainda faltaria caminhar até o nó destino, criando assim a variável F.
        testNode.f = testNode.g + testNode.h;
        
        //Dizemos para o nó em questão 'testNode' quem é o pai dele. No caso é o 'currentNode'.
        testNode.parentNode = currentNode;

        //Adicionamos este nó na lista de nós abertos
        this.openNodes.push(testNode);
      }

      //Agora, com todos os nós mais próximos do currentNode já calculados e adicionados na lista de nós abertos, podemos enfim descobrir quem é o nó com menor custo F. Este será a melhor opção de caminho para chegar no destino.
      this.openNodes.sort(this.byCost);
    }

    //Essa variável path é uma variável auxiliar, que armazenará um array de nós que devemos percorrer para ir do nó inicial firstNode até o nó destino lastNode.
    let path: Node[] = [];
    
    //Se currentNode for diferente de null, então é porque temos um caminho calculado. Então vamos recuperar esse caminho.
    if (currentNode != null) path = this.parsePath(currentNode);

    //Com o array de nós que devemos percorrer para chedar de firstNode até lastNode em mãos, basta retornar na função.
    return path;
  }

  /**** Função getAroundNodes() ****/
  /* Função responsável por gerar os nós mais próximos de um determinado nó. Considere que o nó central, com valor 'A' do desenho abaixo seja o nó atual, e queremos gerar os nós mais próximos dele 'P'. Lembre-se que estamos trabalhando apenas com nós na ortogonal.
  X P X
  P A P
  X P X
  */
  private getAroundNodes(node: Node): Node[] {
    let out: Node[] = [];

    //North
    let n = new Node(new Position(node.position.x, node.position.y - 1), 10, 0, 0, 0, null);
    out.push(n);

    //East
    let e = new Node(new Position(node.position.x + 1, node.position.y), 10, 0, 0, 0, null);
    out.push(e);

    //South
    let s = new Node(new Position(node.position.x, node.position.y + 1), 10, 0, 0, 0, null);
    out.push(s);

    //West
    let w = new Node(new Position(node.position.x - 1, node.position.y), 10, 0, 0, 0, null);
    out.push(w);

    return out;
  }

  /**** Função heuristic() ****/
  // Essa função é responsável por calcular o quanto ainda falta caminhar, partindo de um determinado nó (from) até um nó destino (to).
  private heuristic(from: Node, to: Node): number {
    return Math.abs(from.position.x - to.position.x) + Math.abs(from.position.y - to.position.y);
  }

  /**** Função byCost() ****/
  //Responsável por retornar quem tem o custo maior. A ou B. Em breve escreverei um artigo sobre como ordenar arrays em javascript usando objetos complexos, assim ficará mais fácil entender como essa função funciona.
  private byCost(a: Node, b: Node): number {
    return a.f - b.f;
  }

  /**** Função inCloseNodesList() ****/
  //Essa função é responsável por verificar se um determinado nó está na lista de nós fechados ou não. Se estiver retorna true. Se não estiver, retorna false.
  private inCloseNodesList(node: Node) {
    for (let i = 0; i < this.closeNodes.length; i++) {
      let n = this.closeNodes[i];

      if (n.position.x == node.position.x && n.position.y == node.position.y) return true;
    }

    return false;
  }

  /**** Função parsePath() ****/
  //Responsável por criar o array de nós necessários para chegar do firstNode até o lastNode. Este método é necessário pois quando geramos o caminho na função getPath, este caminho vem como apenas um nó. Mas lembra daquele parâmetro 'parent' do nó? Então, ele é como se fosse o histórico desse nó. Ou seja, se queremos ir do nó A até o nó F, então o getPath vai gerar o nó F, que tem como pai o nó E, que tem como pai o nó D, que tem como pai o nó C, que por sua vez tem como pai o nó B e por fim o nó A. Ou seja A -> B -> C -> D -> E -> F. Esse é o caminho mais curto para ir de A até F.
  private parsePath(node: Node): Node[] {
    let currentNode = node;
    let path: Node[] = [];

    while (currentNode.parentNode != null) {
      let n = currentNode;
      path.push(n);
      currentNode = currentNode.parentNode;
    }

    return path.reverse();
  }
}

Lembre-se: Leia os comentários do código, pois o código está todo comentado, detalhadamente. Isso irá clarear sua interpretação. ;)

---

Enfim… Espero que eu tenha conseguido passar para o leitor, de forma clara e simples, como funciona esse algoritmo de suma importância e que pode ser aplicado em várias situações cotidianas.

Caso você tenha alguma dúvida, comente no texto e tentarei responder da melhor forma possível.

Até a próxima!