[DATA SCIENCE] DAY: 024 - Calculando o coeficiente de correlação de Pearson

💠 Bom dia, boa tarde e boa noite pessoal, tudo bem?

🧘🏼‍♂️ Hoje iremos falar sobre Coeficiente de correlação de Pearson

O coeficiente de correlação de Pearson é um valor entre -1 e 1 que indica o grau de relação linear entre dois conjuntos de dados. Um valor próximo de 1 indica uma relação forte e positiva entre os dados, enquanto um valor próximo de -1 indica uma relação forte e negativa. Um valor próximo de 0 indica a ausência de relação linear entre os dados.
Significado da web

📝 Obs: Irei utilizar o jupyter notebook para a fácil visualização dos gráficos, mas fique a vontade para escolher outro ambiente de sua preferência. Uma sugestão caso não conheça nenhum, tem o colab do google.

1 - Primeiro, podemos usar a notação as para abreviar o nome das bibliotecas e métodos que vamos importar, vamos aplicar a configuração de visualização de alguns gráficos, ler um arquivo CSV e renomear as colunas:

🔍 Para baixar o arquivo que está sendo usado, clique aqui.

💻

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
import seaborn as sns


%matplotlib inline
rcParams['figure.figsize'] = 6, 3
sns.set_style('whitegrid')

caminho = 'O-caminho-do-seu-arquivo/mtcars.csv'
carros = pd.read_csv(caminho)
carros.columns = ['nomes','mpg','cyl','disp', 'hp', 'drat', 'wt', 'qsec', 'vs', 'am', 'qtd_marchas', 'carb']

📝 Obs: O que esse código faz???

• Importação de bibliotecas: O código importa as bibliotecas pandas, matplotlib, seaborn e algumas configurações de matplotlib.
• Configuração de visualização: O tamanho do gráfico é definido e o estilo de visualização é configurado como whitegrid.
• Carregamento do dataset: O arquivo csv "mtcars" é carregado usando a função read_csv do pandas e atribuído à variável carros.
• Renomeação de colunas: As colunas do dataset são renomeadas de acordo com a lista fornecida.

Vamos importar a função pearsonr da biblioteca scipy.stats. Essa função é utilizada para calcular o coeficiente de correlação de Pearson entre dois conjuntos de dados.

💻

from scipy.stats.stats import pearsonr

Obs: Lembre-se de escolher variáveis que seguem os pressupostos:

• Apresentar distribuição normal
• Variáveis contínuas
• Relação linear

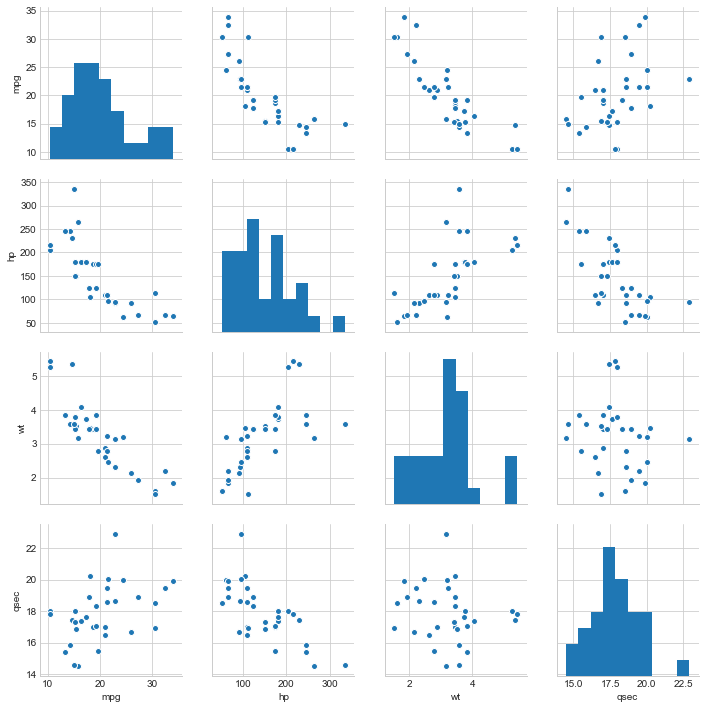
2 - Vamos montar um gráfico que mostra a relação entre cada par de variáveis e que ajuda a identificar qualquer tendência ou relação linear entre os dados:

💻

X = carros[['mpg', 'hp', 'wt', 'qsec']]
sns.pairplot(X)

📝 Obs: O que esse código faz???

• Seleção de colunas: As colunas mpg, hp, wt e qsec são selecionadas do DataFrame carros e atribuídas à variável X.
• Criação do gráfico de dispersão: A função pairplot() do seaborn é usada para criar um gráfico de dispersão para cada par de variáveis contidas no DataFrame X.

Gráfico gerado:

3 - Também podemos utilizar o scipy para calcular o coeficiente de correlação de Pearson:

💻

mpg = carros['mpg']
hp = carros['hp']
qsec = carros['qsec']
wt = carros['wt']

coeficiente_pearsonr, p_valor = pearsonr(mpg, hp)
print('PearsonR Correlation Coefficient {:0.3}'.format(coeficiente_pearsonr))

Saída do código:

PearsonR Correlation Coefficient -0.776

📝 Obs: O que esse código faz???

• Seleção de colunas: As colunas mpg, hp, wt e qsec são selecionadas do DataFrame carros e atribuídas às variáveis mpg, hp, qsec e wt respectivamente.
• Cálculo do coeficiente de correlação de Pearson: A função pearsonr é chamada e passa as variáveis mpg e hp como argumentos. O resultado é atribuído às variáveis "coeficiente_pearsonr" e p_valor.
• Impressão do coeficiente de correlação: O coeficiente de correlação é impresso com 3 casas decimais usando a função format().

💡 Podemos reaplicar a mesma lógica nas outras colunas para identificarmos a diferença entre as correlações:

💻

Utilizando o coeficiente de Pearson na coluna wt

coeficiente_pearsonr, p_valor = pearsonr(mpg, wt)
print('PearsonR Correlation Coefficient {:0.3}'.format(coeficiente_pearsonr))

Saída do código:

PearsonR Correlation Coefficient -0.868

💻

Utilizando o coeficiente de Pearson na coluna qsec

coeficiente_pearsonr, p_valor = pearsonr(mpg, qsec)
print('PearsonR Correlation Coefficient {:0.3}'.format(coeficiente_pearsonr))

Saída do código:

PearsonR Correlation Coefficient 0.419

4 - Também podemos utilizar o pandas para calcular o coeficiente de correlação de Pearson:

💻

corr = X.corr()
corr

Saída do código:

             mpg	       hp	       wt	    qsec
mpg	1.000000	-0.776168	-0.867659	0.418684
hp     -0.776168	 1.000000	 0.658748      -0.708223
wt     -0.867659	 0.658748	 1.000000      -0.174716
qsec	0.418684	-0.708223	-0.174716	1.000000

📝 Obs: O que esse código faz???

• Cálculo da correlação: A função corr() é aplicada ao DataFrame X para calcular as correlações entre as variáveis.
• Atribuição do resultado: O resultado é atribuído à variável corr.
• Impressão do resultado: O DataFrame corr é impresso na tela, mostrando os valores de correlação entre as variáveis contidas no DataFrame X.

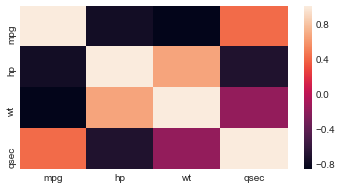
5 - Por último não menos importante, podemos visualizar o coeficiente de Pearson com a beleza dos gráficos do Seaborn:

💻

sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values)

📝 Obs: O que esse código faz???

• Criação do mapa de calor: A função heatmap() do seaborn é utilizada para criar um mapa de calor a partir do DataFrame corr.
• Definição dos rótulos do eixo x e y: os rótulos do eixo x e y são definidos como os nomes das colunas do DataFrame corr usando os atributos columns.values.
• Exibição do mapa de calor: O mapa de calor é exibido na tela mostrando as correlações entre as variáveis contidas no DataFrame X com diferentes cores, onde as cores mais escuras indicam uma maior correlação.

Gráfico gerado:

🌊 Espero que tenham gostado do conteúdo, amanhã iremos aprender como usar o SPearman e Qui-quadrado!

🚀 Vejo vocês amanhã, tenham uma ótima semana!