[PROIBIDO PARA SÊNIORS] - Encontrando um uso "de verdade" para tabelas-verdade · obrunoanastacio

Se você está na faculdade, pode ser que você tenha tenha feito bico pra matérias como Matemática Discreta ou Lógica Proposicional (não sei com que nome esse "pacote" chegou até você).

Mas o meu humilde conselho é: preste atenção nessas aulas. Parece que não, mas elas vão te ajudar muito lá na frente.

Hoje eu trago um exemplo dos mais bobos sobre como isso vai te destravar na hora de codar.

(Lembrando que este exemplo bobo é proibido para sêniors. O objetivo aqui não é discutir quantos ifs tem no código do juninho e nenhum desses outros assuntos do Olimpo. Se você é chegado ao vinho da "filosofia do código", tenha um pouco de paciência com quem está começando).

Calma, Suzana!

O Exemplo

Suponhamos que você está escrevendo uma rotina bem simples, que precisa definir para quem uma linha de crédito será ou não liberada. Abstraí ao máximo para irmos direto ao ponto.

No código abaixo, para liberar o crédito para o cliente, você precisa validar se este tem saldo em conta e nome limpo.

boolean LiberarCredito(Cliente cliente){
        if(cliente.getSaldo() > 0{
            if(cliente.getNomeLimpo()){
                return true;
            }else {
                return false;
            }
        }else {
            return false;
        }    
    }

Se você reparar, no código acima, estamos escrevendo duas vezes a mesma linha return false.: toda vez que você precisa repetir uma linha de código, você deveria ligar o sinal de alerta.

Refatorando o código utilizando tabelas verdade

Para quem não lembra, as tabelas verdade são úteis para verificarmos todas as possibilidades lógicas de uma proposição ou de um conjunto de proposições. Na imagem abaixo, verificamos em quais cenários a conjunção de p e qé verdadeira:

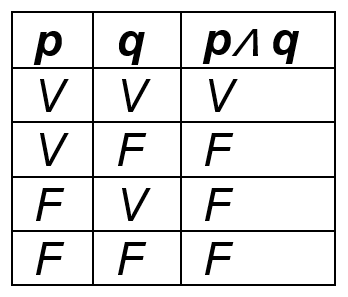
E isso tem tudo a ver com o nosso código!

Imagine que p é a verificação de saldo e q é a verificação de nome limpo. Sequer precisamos desenhar uma tabela verdade "tradicional" para verificarmos. Eu fiz a minha nos comentártios do código mesmo. E fiz de propósito: o objetivo é mostrar que quando você estiver travado na lógica do seu código, você poder resolver em um bloco de notas qualquer. Basta raciocinar.

    //TABELA VERDADE:
    //if(cliente.getSaldo() > 0                         V  V  F  F
    //cliente.getNomeLimpo()                            V  F  V  F
    //LiberarCredito(Cliente cliente);                  V  F  F  F
    
    //CENÁRIOS:
    //Cliente tem saldo, mas não tem nome limpo - não liberar
    //Cliente não tem saldo, mas tem nome limpo - não liberar
    //Cliente tem saldo e tem nome limpo        - LIBERAR!
    //Cliente não tem saldo nem nome limpo      - não liberar

O que a nossa tabela verdade acabou de mostrar só existe uma situação em que podemos liberar credito ao cliente. Em todas as outras, devemos recusar. Sendo assim, um if já seria o bastante. O que precisamos validar é se a única situação passível de liberação se cumpre ou não.

    boolean LiberarCredito(Cliente cliente){
        if(cliente.getSaldo() > 0 && cliente.getNomeLimpo())
            return true;
        else return false;
    }

Indo além

O código acima poderia ficar ainda mais "limpo":

     boolean LiberarCredito(Cliente cliente){
         return cliente.getSaldo() > 0 && cliente.getNomeLimpo();
    }

E isso tem tudo a ver com mátemática discreta. Como já escrevi neste post, o que acontece aqui é o uso do Modus Ponens, ou Modo de Afirmação. Esta é uma regra de inferência lógica que diz o seguinte:

Se a premissa é verdadeira, então a consequência é verdadeira
A premissa é verdadeira.
Logo, a consequência é verdadeira.

Em outras palavras:

Se a premissa cliente.getSaldo() > 0 && cliente.getNomeLimpo() é verdadeira, então a consequência LiberarCredito == true é verdadeira
A premissa cliente.getSaldo() > 0 && cliente.getNomeLimpo()é verdadeira.
Logo, a consequência LiberarCredito(Cliente cliente) == true é verdadeira.
E se a premissa cliente.getSaldo() > 0 && cliente.getNomeLimpo()for falsa, LiberarCredito(Cliente cliente) == false

Conclusão

Desprezada por muitos, a Matemática Discreta tem grande uso na formação do raciocínio lógico do programador. E o mínimo que se espera de um iniciante é que consiga aplicar a teoria básica, que não depende de frameworks e linguagens da moda. Os exemplos acima são aplicáveis em qualquer das principais linguagens atuais de mercado.

Para ir além, recomendo o livro "Fundamentos Matemáticos para a Ciência da Computação", da Judith Gersting. No livro, ela vai explicando matemática discreta e dando exemplos com snippets de código, onde fica bem claro o uso prático de tudo isso.

Ótima dica! Apesar de eu ter aprendido essa dica por simples experiência de ver código de gente mais esperta que eu (eu sou bem júnior ainda) e copiado a ideia só pra deixar o código mais enxuto e legível, eu nunca tinha visto como isso poderia ser representado com lógica proposicional, nem nunca vi nada de lógica proposicional ser convertido em código.

Mas, pra ser sincero, pelo menos até onde eu estudei sobre lógica, o tanto que ela pode ajudar na resolução de problemas algorítmicos ainda é um tanto limitado. Pode fazer toda a diferença pra quem tá começando com programação e ainda se enrola com estruturas de if/else, loops e coisas do tipo, mas ainda não consigo ver como essas estruturas formais ajudariam a reverter uma lista encadeada, por exemplo.