Executando verificação de segurança...
5
meritissimo1
3 min de leitura ·

Estrutura de Dados #1

Já faz um tempo que não escrevo sobre esse assunto mas, antes tarde do que nunca 🤝

Continuando da onde eu parei (Estrutura de Dados #0) hoje eu quero falar sobre Complexidade de Algoritmos e por que você deveria pensar duas vezes antes de colocar um While/for dentro do outro.

Já deixando um disclaimer, eu não sou nenhum professor universitário que entende 100% do assunto, sou só um estudante que gostou da matéria Estrutura de Dados :).

O estudo de Complexidade de Algoritmos envolve analisar o tempo de execução de determinado algoritmo e por isso, esse assunto também pode ser chamado de Tempo de Complexidade ou em English - Time Complexity. A importância de se estudar quanto tempo seu algoritmo levará pra ser executado numa determinada situação parece ser bastante auto explicativa, mas dando um exemplo, imagine que você é um(a) engenheiro(a) de software da Twitch e que agora você precise ordenar todos os canais online baseado no número de espectadores de cada canal. Dependendo da forma que você faça isso, talvez o seu algoritmo leve muito tempo para terminar a execução gastando muito recurso de processamento, e levando em consideração que estamos falando de uma grande empresa com muitos usuários e muitos dados, isso seria bem ruim. Nesse caso, você teria que antes mesmo de começar a escrever qualquer código, analisar como o algoritmo se comportaria no pior caso possível e essa analise é feita usando uma notação matemática (eu acho que exclusiva da computação) conhecida como Notação Big O, ou O Grande. A Notação Big O foca em analisar o comportamento do algoritmo no pior caso possível. Existem outras notações para melhor caso e caso médio, mas vamos ver aqui somente a Big O mesmo. Aqui são algumas exemplos:

  • O(1) -> As instruções são constantes, independente do n° de elementos.
  • O(n) -> No pior caso teremos n instruções e o crescimento é linear.
  • O(n²) -> No pior caso teremos n² instruções e o crescimento é exponencial.
  • O(log(n)) -> No pior caso teremos log2(n) = x, onde x é o n° de instruções e o crescimento é esse aqui da foto haha.

Big O Notation

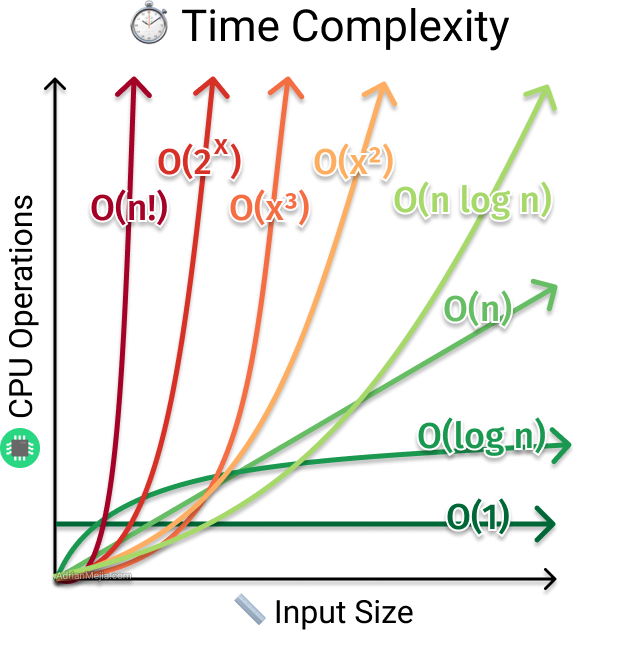
A forma como eu aprendi complexidade foi analisando algoritmos e é o que nós vamos fazer agora!

Trouxe aqui 3 algoritmos de ordenação bem conhecidos: Insertion Sort, Selection Sort, Bubble Sort :)

Para entender a complexidade de um algoritmo, precisamos entender o que ele faz e principalmente COMO ele faz. Então começando pelo Insertion Sort, vamos escrever em poucas palavras o que ele faz e como, de uma forma que já nos de a resposta da complexidade

  • Insertion Sort: Para cada elemento, busca-se a posição correta no vetor. Ou seja, para cada N elementos temos que percorrer N posições, Logo, sua complexidade é O(n²).

Perceba que nós chegamos na complexidade sem escrever nenhuma linha de código! basta dizer da forma certa o que ele faz e como. Vamos tentar com os outros.

  • Selection Sort: Para cada posição, busca-se o elemento correto no vetor. Ou seja, Para cada N posições temos que percorrer N elementos, Logo, sua complexidade é O(n²).

e por fim,

  • Bubble Sort: Para cada par de elementos, busca-se a posição correta relativa no vetor. Ou seja, Para cada N pares de elementos temos que percorrer N posições, Logo, sua complexidade é O(n²).

Só com base nessas simples frase, qualquer pessoas que não seja um programador chaves haha, consegue implementar os algoritmos acima em QUALQUER LINGUAGEM! Inclusive, recomendo fortíssimo vocês implementarem esses algoritmos até pra entenderem o que eu falei lá no início, fica aí o desafio.

Exercitem essa dica de resumir o algoritmo em poucas palavras já deixando claro a complexidade e se quiserem, respondam aqui como fizeram 😁

Alguns materiais adicionais:
Insertion Sort 💃
Selection Sort 💃
Bubble Sort 💃

1
RafaelRNF

Que fantástico esses 3 vídeos, muito bom... Isso sim é mostrar algo com uma visão bem diferente, sensacional demais...
Eu estudei isso num curso e é incrível como esses 3 vídeos me fizeram enxergar num 'formato' completamente novo e simples, abstrair algo além de só números ajuda muito.

A, e claro, ótimo conteúdo, mas acho que seria melhor se você colocasse um exemplo que tivesse outro Big O.

1
Kaindall

Pensando por exemplo numa simples leitura de documento em que precisamos buscar uma palavra em específico.

A primeira iteração seria sobre todas as linhas, a segunda iteração seria sobre todas as palavras desta linha buscando a específica. Qual seria a alternativa, senão "for" encadeado?

Aliás, sei que há também aquelas a lógica vetorial para tornar estas buscas mais rápidas, como se fossem "índices" de um livro que lendo ele você já sabe aonde está cada coisa do livro propriamente dito, mas não se aplica.

1
flashzz

Uma busca linear na maioria dos casos vai ser O(N), pois você precisa percorrer todos os elementos de uma lista, vetor e etc. Nesse caso do documento você vai utilizar um for encadeado mas vai fazer uma busca linear no documento, pois vai "varrer" ele uma só vez, considerando que ele tenha N palavras, você vai fazer N operações para realizar a busca no pior caso, portanto o for encadeado não é responsável por deixar a quantidade de operações quadrática em relação ao tamanho da entrada nesse caso.
Com relação a otimização da busca, ela pode ser feita quando sua lista de elementos é ordenada, podendo assim utilizar a busca binária.

1
1
meritissimo1
Autor
Autor

Um loop somente, um while(i < n) por exemplo, no pior caso ele vai percorrer N elementos, o porquê seria, imagina que tu ta buscando um numero e ele tá no final do vetor (pior caso), terianos que percorrer todos os elementos pra chegar nesse valor, ou seja N elementos, por isso a complexidade é O(n).

Caso fosse um loop dentro do outro while (i < linhas)
while (j < colunas)

no pior caso a complexidade seria O(n²). Olhando pra esse loop de cima, imagina que estamos buscando um elemento numa matrix 4x4 e esse elemento tá no final da matrix, o elemento 4,4. Teriamos que percorrer N linhas no primeiro while e N colunas no segundo while, por isso n².

Valeu pela pergunta e espero ter respondido 😁✌️