Insights de "O Andar do Bêbado" sobre Ciência de Dados

Revisão do livro de Leonard Mlodinow "O Andar do Bêbado: Como o Acaso Determina Nossas Vidas", apontando e explicando relações com a Ciência de Dados.

A ideia principal é apresentar explicações [muito simplificadas] sobre as leis do acaso mencionadas no livro, bem como estabelecer relações com o que sei sobre os temas centrais da ciência de dados (você pode esperar um foco em Inteligência Artificial). No pior cenário, você acabará lendo uma resenha sobre o livro.

Aqui fica minha recomendação, e você pode saber mais sobre o livro aqui.

Para mim, foi uma leitura muito boa. Assim como uma distribuição normal, o livro começa de maneira geral, falando sobre aleatoriedade e convencendo da sua importância e presença na vida cotidiana. No meio, as coisas ficam mais complexas, com explicações e contextos históricos das principais leis do assunto. Para o final, o autor volta ao efeito do acaso no dia a dia, agora com muito mais contexto para fornecer ao leitor.
No geral, percebi que foi uma conversa sincera sobre o não determinismo da realidade.

Aviso: Não sou especialista e este post é generalista. Não leve o que digo como um fato. Na verdade, vou apreciar se você apontar meus erros. Obrigado.

A Constituição da Probabilidade

Pode ser interessante começarmos com algumas leis. Isso me ajudou muito e tentei fazer alguns exemplos usando o Excalidraw.

Essas três leis — como o que aconteceu com aquele cara Newton — têm um grande impacto em como percebemos a probabilidade, especialmente na vida cotidiana. E o autor provou isso de muitas maneiras, uma delas citando um experimento com a dinâmica dada:

Um grupo de pessoas recebeu a mesma descrição breve sobre uma mulher (a descrição descreve propositalmente uma mulher que pode trabalhar em um banco e apoiar o feminismo) e depois tiveram que classificar algumas afirmações sobre ela. Um exemplo muito simplificado das afirmações seria:

• Ela trabalha em um banco
• Ela apoia o movimento feminista
• Ela trabalha em um banco e apoia o movimento feminista

Todos os detalhes podem estar confusos agora, mas o foco está na disposição das afirmações. A última foi votada como a mais provável de ser verdadeira, quebrando as leis mostradas acima, porque "A probabilidade de ambos os eventos A e B ocorrerem é sempre menor do que a probabilidade de um deles sozinho".

Isso não apenas mostra quão intuitiva nossa opinião pode ser, desrespeitando completamente a lógica da probabilidade, mas o experimento também pode demonstrar como, com mais detalhes [aparentemente verdadeiros], nós humanos tendemos a acreditar que uma afirmação é verdadeira E mais provável de ser verdadeira do que outras.

Hoje em dia, isso se torna visível com a capacidade de convencimento de modelos generativos como o ChatGPT ou Bard. Poderíamos dizer que quanto menos contexto e mais o modelo é comandado a gerar, mais improvável será que o resultado seja completamente preciso. Embora isso não seja exatamente o que as pessoas sentem quando o ChatGPT escreve um artigo completo com um monte de palavras bonitas que "parecem" estar corretas.

Analisando Eventos

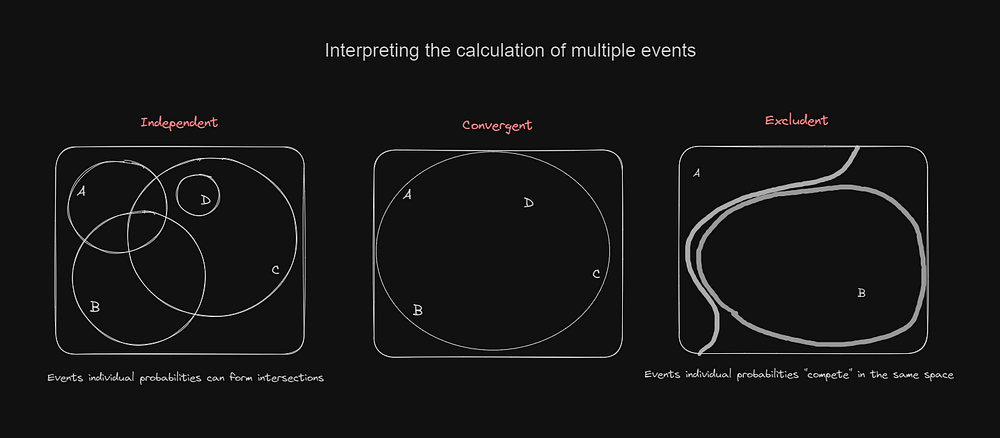
Agora vamos nos familiarizar com essas palavras reservadas da linguagem probabilística: Espaço amostral e Evento. Além disso, devemos entender como múltiplos eventos podem se relacionar dentro de um espaço amostral, afinal, essa é a dinâmica fundamental para calcular a probabilidade.

A especialidade dessa análise para a IA está no processo de limpeza/normalização de dados e no processo de definir as features que o modelo irá considerar. Em um treinamento supervisionado, isso pode ser mais óbvio, já que o cientista deve analisar o conjunto de dados e calcular as features. Mas esse processo não é menos importante para aprendizado não supervisionado, como em alguns LLMs como o GPT-4 ou o Llama-2.

Ao fazer esse tipo de análise, alguns pontos importantes a considerar são:

• A probabilidade de um evento depende diretamente do número de maneiras pelas quais ele pode ocorrer
• Como os eventos se relacionam entre si? Suponha que um dos eventos seja verdadeiro, os outros se tornam mais propensos a ser verdadeiros? Pode ser uma convergência. Se nada mudar, pode ser independente. E termina com a exclusão se forem impossíveis de ocorrer juntos.
• Em um espaço amostral específico, como as novas informações alteram o espaço e as probabilidades individuais dos eventos?

Seguindo o autor, vamos pegar o exemplo do jogo de Monty Hall. Nesse jogo, pode haver 3 portas, todas fechadas, e atrás de apenas uma delas está o prêmio, atrás das outras só há derrota.

Você escolhe uma porta, mas antes de revelar o que está atrás da sua porta, o apresentador abre uma das portas não escolhidas (que ele sabe que não tem prêmio). Agora, restando duas portas, ele pergunta se você quer mudar.

É melhor mudar ou não? Qual oferece a melhor chance, mudar ou manter?

Não há mistério aqui, é mais provável encontrar o prêmio se você trocar de porta. E isso pode ser explicado pela probabilidade clássica: O importante aqui é a sua primeira escolha, em nosso exemplo, sua primeira escolha tem 1/3 de chance de acertar a porta com o prêmio, enquanto tem 2/3 de chance de errar. Depois que o apresentador revela uma porta "aleatória", restam apenas 2, e como você escolheu muito provavelmente a porta sem prêmio (2/3 de chance de escolher uma porta sem prêmio), trocando você acabaria com a porta do prêmio.

Inicialmente, não consegui entender isso porque estava considerando a ação do apresentador de abrir uma das portas como uma redução do espaço amostral, mas isso não é exatamente o caso, isso muda a dinâmica, mas não afeta as chances da sua primeira escolha, e isso é o que importa.

Abordagens para a Probabilidade

Até agora, percorremos principalmente os caminhos seguros da probabilidade clássica, onde exemplos com dados e moedas são frequentemente usados, mas as coisas ficam muito interessantes na probabilidade empírica, também mais próxima do que é usado para o treinamento de modelos de IA hoje em dia.

Na probabilidade empírica, começamos a interpretar espaços amostrais como algo contínuo, trazendo à mente um novo conjunto de pontos:

• Eventos bem-sucedidos agora são contados como uma frequência dentro do espaço amostral contínuo
• Quanto maior você escolher que seja seu espaço amostral (quanto mais experimentos você fizer), mais precisa será sua probabilidade resultante
• Quantas vezes eu preciso lançar uma moeda para validar a probabilidade de 50% de chance para cada lado?
• Como o espaço amostral é contínuo e precisa ser cortado por questões de praticidade, nossa análise pode ser enviesada por um corte inadequado. Ou talvez padrões se tornem visíveis onde apenas o acaso deveria existir.

Há muito nessa abordagem empírica, e basicamente tudo se encaixa no treinamento e avaliação de modelos de IA. Às vezes, parece descrevê-lo completamente, na verdade.
Pense em um processo em que você deseja analisar um conjunto de dados com 1 bilhão de linhas, uma após a outra, e após cada análise avaliar quão próximo você está de uma precisão esperada de probabilidade, mantendo o melhor resultado para ser usado em avaliações posteriores mais gerais. Bem, isso pode ser apenas um modelo sendo treinado.

Inteligência Artificial e Estatística

Todo o campo da IA é como — não "apenas" — outro uso prático de estatísticas.

Você pode notar que muitos termos de estatística ainda não foram mencionados: média, correlação, covariância, desvio padrão…
Provavelmente, você esperava vê-los, já que são extremamente usados e conhecidos. Então, tentando fazer algo pelo menos diferente, mas ainda mencionando-os, deixei para esta parte final, agrupados juntos.

Se separarmos o treinamento de um modelo em etapas, todas elas serão baseadas em probabilidade e estatística:

• Análise e coleta de dados: histogramas de frequência, distribuição normal, média, desvio padrão, grau de correlação… são usados para limpar vieses, normalizar o conjunto de dados e definir as principais features para o treinamento.
• Definição de hiperparâmetros: Quantidade de entradas, neurônios, camadas, saídas, função de ativação, função de custo, a quantidade pela qual o modelo back propagate suas mudanças durante o treinamento… a maior parte disso parece ser escolhida do nada (talvez sejam), mas existem algumas teorias de probabilidade que dão pistas sobre como a topologia neural deve parecer dado o resultado procurado. Por exemplo: a distribuição Bernoulli poderia dizer algo sobre quantas vezes você deve testar para alcançar uma determinada proporção de probabilidade; O número de camadas dá um efeito de curva à regressão, usado para casos polinomiais; …
• Treinamento: funções de ativação que produzem resultados probabilísticos são usadas no cálculo para cada neurônio da rede neural. O resultado final é avaliado em uma função de custo (às vezes muito semelhante à fórmula do desvio padrão). Esse processo usa o algoritmo de gradiente descendente para chegar à melhor função generalista (nem sempre correta, mas a mais próxima do certo que pode chegar para cada exemplo treinado).
• Avaliação: após treinado, um modelo precisa ser amplamente testado, calculando sua proporção de probabilidade, margem de erro, acertividade testada, precisão testada. Gerando uma nova gama de dados para serem analisados, assim como o conjunto de dados usado para treinamento.

Conclusão

A conclusão do livro não é sobre probabilidade, é sobre a vida, e por isso só a experiência de ler o livro valeu a pena. Mas gostei de como me fez pensar em meus estudos no campo da Ciência de Dados e me trouxe até este momento.
Estou feliz por ter escrito este post e agradecido por você ter reservado um tempo para lê-lo.

Obrigado.