🗣️ Seria a comunicação algo universal?

Bem vindo! 👋🙋‍♂️

Neste artigo eu gostaria de debater sobre a possibilidade das linguagens serem algo universal. Em outras palavras, imagine que você criou uma nova linguagem para comunicação na sua cabeça neste exato momento e você fica maravilhado com a criação semântica e sintática que você desenvolveu. Você começa a escrever um livro gigantesco de aproximadamente 60 mil páginas com essa nova linguagem e, em seguida, faz o árduo trabalho de traduzir esse grande amontoado de informações para uma linguagem mais acessível - como o português ou inglês. Infelizmente, nesse cenário hipotético, você acaba falecendo antes de publicar um dicionário mostrando o que as palavras representariam na língua mais acessível. Com base nessa hipotética história, haveria como moldarmos uma espécie de programa que fizesse o papel de dicionário, isto é, conseguisse ligar uma ou mais palavras da sua linguagem com uma ou mais palavras desse idioma mais falado, mesmo após o seu falecimento?

Vamos mergulhar nesse interessante assunto que está relacionado com uma peça importante da empresa Google (Alphabet). Contudo, vamos por partes.

Um pouco de história: Google Tradutor.

Em maio de 2014, o Google adquiriu o Word Lens para melhorar a qualidade da tradução visual e de voz. Ele é capaz de digitalizar texto ou imagem usando o dispositivo e traduzi-lo instantaneamente. Além disso, o sistema identifica automaticamente idiomas estrangeiros e traduz a fala sem exigir que os indivíduos toquem no botão do microfone sempre que a tradução da fala for necessária.

Em novembro de 2016, o Google fez a transição de seu método de tradução para um sistema chamado tradução automática neural. Ele usa técnicas de aprendizado profundo para traduzir frases inteiras de uma só vez, o que foi medido para ser mais preciso entre inglês e francês, alemão, espanhol e chinês. Nenhum resultado de medição foi fornecido pelos pesquisadores do Google para GNMT do inglês para outros idiomas, de outros idiomas para o inglês ou entre pares de idiomas que não incluam o inglês.

A partir de 2018, traduz mais de 100 bilhões de palavras por dia. Em 2017, o Google Tradutor foi usado durante uma audiência no tribunal, quando funcionários do Tribunal de Magistrados de Teesside não conseguiram contratar um intérprete para o réu chinês. No final de setembro de 2022, o Google Tradutor foi descontinuado na China continental, o que o Google disse ser devido ao "baixo uso".

Parte 1: O Modelo de tradução automática neural com atenção.

Nessa parte eu terei que me esforçar para explicar esse modelo. Mesmo sem ser um especialista no assunto, tentarei mostrar como esse modelo funciona. Eu não irei adentrar na matemática, mas no artigo completo você poderá ter total acesso a essa parte e, devido a esse motivo, coloquei nas referências bibliográficas.

A primeira coisa que você precisa entender é que o modelo aprende com base em sentenças. Veja um exemplo abaixo.

Primeira sentença - Espanhol:

Si quieres sonar como un hablante nativo, debes estar dispuesto a practicar diciendo la misma frase una y otra vez de la misma manera en que un músico de banjo practica el mismo fraseo una y otra vez hasta que lo puedan tocar correctamente y en el tiempo esperado.

Primeira sentença - Inglês:

If you want to sound like a native speaker, you must be willing to practice saying the same sentence over and over in the same way that banjo players practice the same phrase over and over until they can play it correctly and at the desired tempo.

Depois de separar as sentenças, seria necessário colocar algum tipo de marcador para que o processamento dos dados seja feita de forma cautelosa e sem muita possibilidade de algo ser dúbio. Note que nesta estapa estamos tratando de algo chamado normalização (processo de aplicação das normas, com o intuito de facilitar o acesso a qualquer atividade específica). Veja abaixo como isso pode ser feito.

Inicialmente teriamos algo como:

¿Todavía está en casa?

E então o 'marcador' adicionado seria algo como:

[START] ¿ todavia esta en casa ? [END]

Depois que um processo de normalização das frases foi aplicado, podemos agora passar para uma parte interessante, onde as frases serão comvertidas em números. Essa parte é feita utlizando a biblioteca Tensorflow com tf.keras.layers.TextVectorization. O resultado da transferência de frases para números é algo como:

array([[   2,    9,   17,   22,    5,   48,    4,    3,    0,    0],
       [   2,   13,  177,    1,   12,    3,    0,    0,    0,    0],
       [   2,  120,   35,    6,  290,   14, 2134,  506, 2637,   14]])

Os IDs de token retornados são preenchidos com zeros. Isso pode ser facilmente transformado em uma máscara:

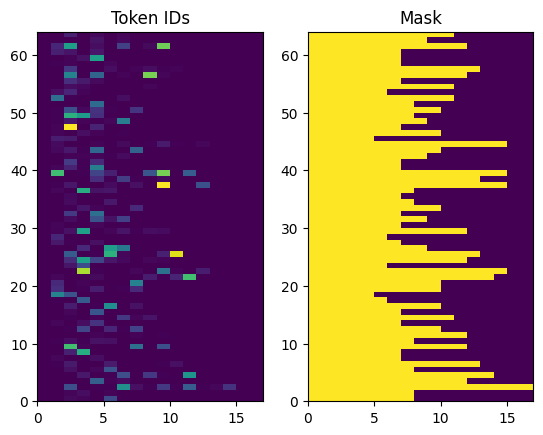
Agora, teremos de nos ater ao modelo de Encoders e Decoders:

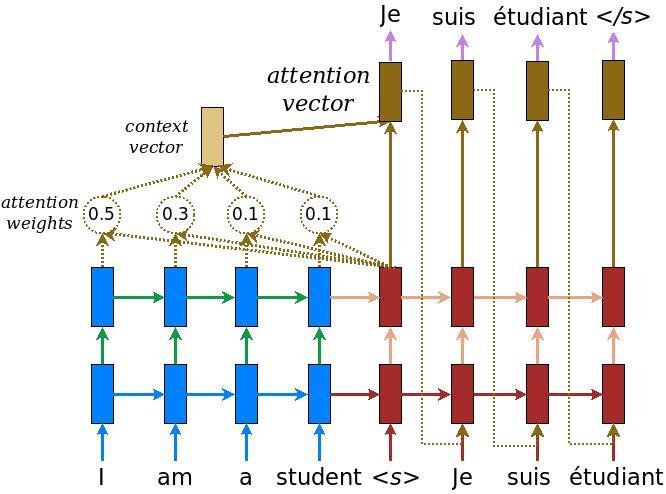
O codificador, em azul, retorna seu estado interno para que seu estado possa ser usado para inicializar o decodificador. Também é comum que um RNN retorne seu estado para que possa processar uma sequência em várias chamadas. Você verá mais sobre como construir o decodificador.

O trabalho do decodificador é gerar previsões para o próximo token de saída. O decodificador recebe a saída completa do codificador.
1° - Ele usa um RNN para rastrear o que gerou até agora.
2° - Ele usa sua saída RNN como a consulta para chamar a atenção sobre a saída do codificador, produzindo o vetor de contexto.
3° - Ele combina a saída RNN e o vetor de contexto usando a Equação 3 (abaixo) para gerar o "vetor de atenção".
4° - Ele gera previsões logit para o próximo token com base no "vetor de atenção".

Algo que é de suma importância para o modelo é o processo de atenção. Isso mostra quais partes da frase de entrada chamam a atenção do modelo durante a tradução. A atenção pega uma sequência de vetores como entrada para cada exemplo e retorna um vetor de "atenção" para cada exemplo. Esta camada atenção é semelhante a um layers.GlobalAveragePoling1D mas a camada de atenção executa uma média ponderada neste exemplo.

Veja algumas figuras de sua atuação:

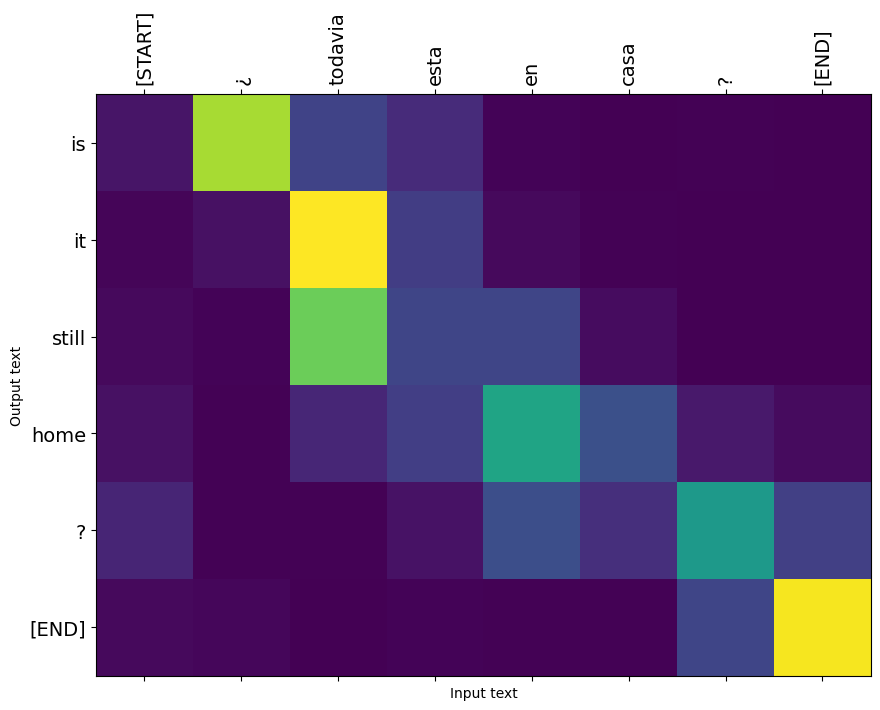
Nesta outra figura, temos o modelo de atenção para uma frase.

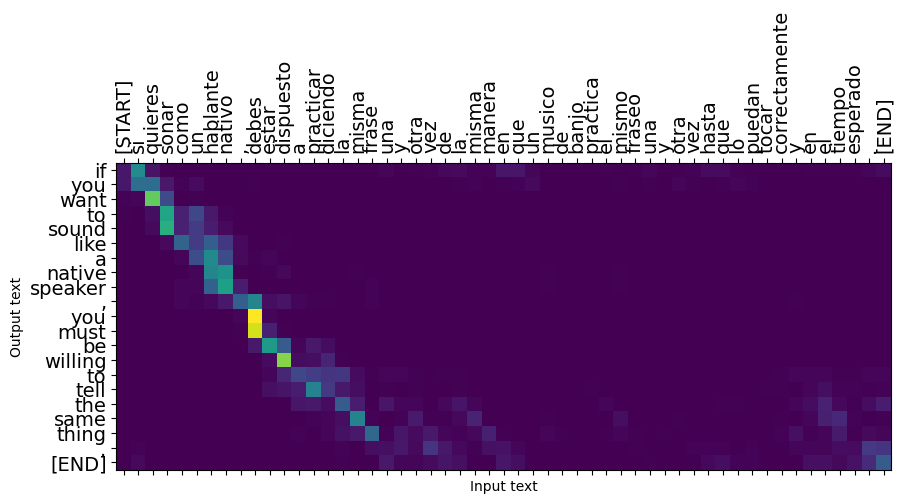
Veja que estamos entrando em um terreno novo: estamos conseguindo mapear estruturas de uma linguagem em outra! quase que como uma matriz de transformação. Guarde essa informação, pois ela será necessário no futuro.

Além disso, veja que, respondendo o questionamento do início, provavelmente seria possível mapear o seu idioma criado para outra línguagem de mais fácil acesso. Mas em relação a linguagens que nunca tivemos um contato antes? Ou melhor dizendo, se você não tivesse feito a tradução das 60 mil páginas para essa linguagem mais acessível, ainda seríamos capazes de entender a estrutura criada somente com um livro de 60 mil páginas que não entendemos?

seguimos em frente...

Parte 2: A lei de Zipf

A lei de Zipf é uma lei empírica formulada usando estatística matemática que se refere ao fato de que, para muitos tipos de dados estudados nas ciências físicas e sociais, a distribuição de frequência de classificação é uma distribuição de relação inversa. A lei leva o nome do linguista americano George Kingsley Zipf , que a popularizou e procurou explicá-la, embora não afirmasse tê-la originado. O estenógrafo francês Jean-Baptiste Estoup parece ter notado a regularidade antes de Zipf.

A lei de Zipf foi originalmente formulada em termos de lingüística quantitativa, afirmando que, dado algum corpus de expressões de linguagem natural, a frequência de qualquer palavra é inversamente proporcional à sua classificação na tabela de frequência. Assim, a palavra mais frequente ocorrerá aproximadamente duas vezes mais que a segunda palavra mais frequente, três vezes mais que a terceira palavra mais frequente, etc.

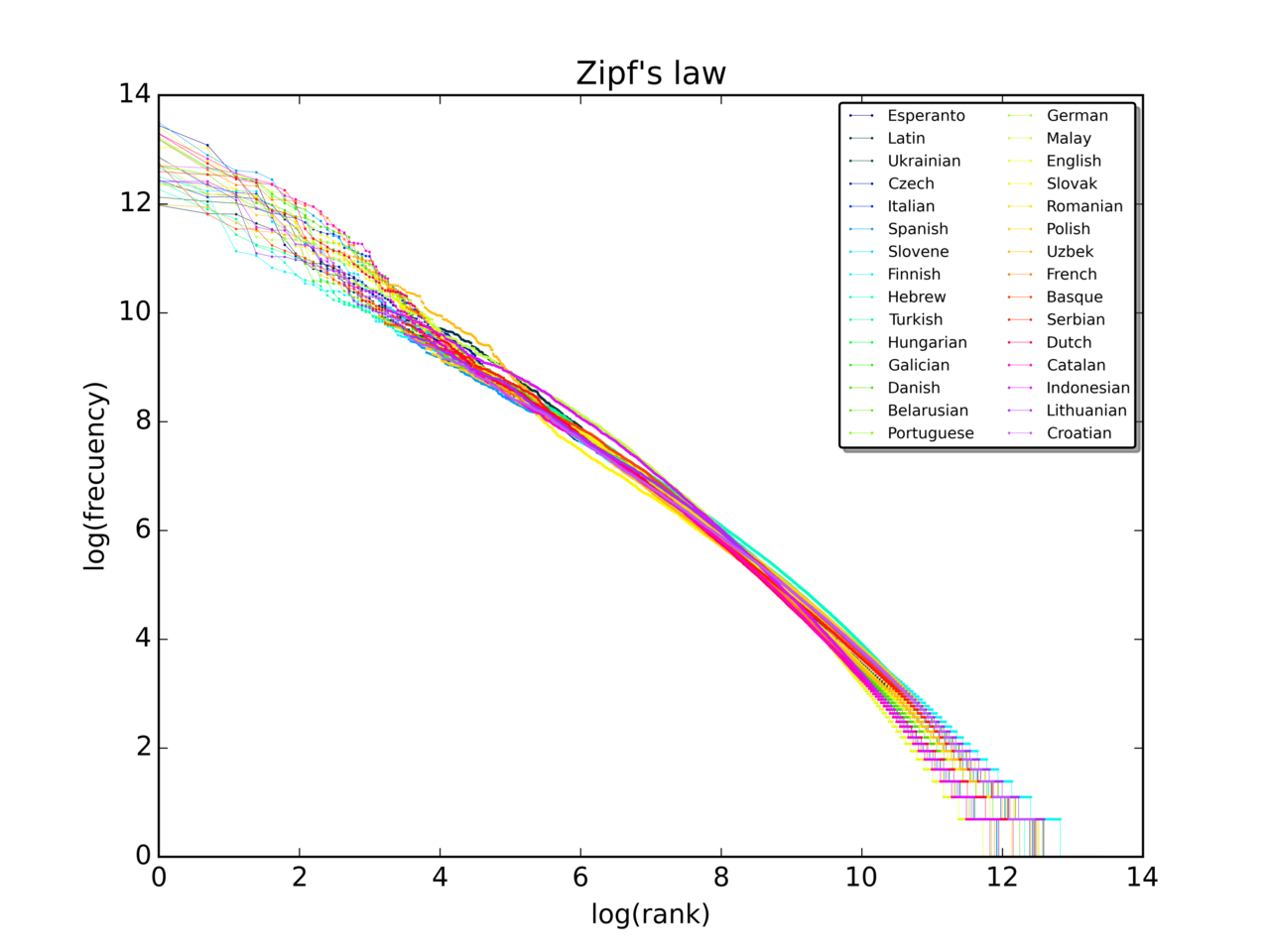
Os testes de adequação mostram que apenas cerca de 15% dos textos são estatisticamente compatíveis com esta forma da lei de Zipf. Pequenas variações na definição da lei de Zipf podem aumentar esse percentual para cerca de 50%. A lei também pode ser escrita como:

onde H(N,s) é o N-ésimo número harmônico generalizado

Nas línguas humanas, as frequências das palavras têm uma distribuição muito pesada e, portanto, podem ser modeladas razoavelmente bem por uma distribuição Zipf com um s próximo de 1. Desde que o expoente s exceda 1, é possível que tal lei seja válida para um número infinito de palavras, pois se s > 1, então a função zeta de Riemann converge.

Embora o padrão quase-Zipfianas seja válida para todas as línguas, mesmo as não naturais como o Esperanto, a razão ainda não é bem compreendida. O princípio do menor esforço é uma explicação possível: o próprio Zipf propôs que nem os falantes nem os ouvintes que usam uma determinada língua querem trabalhar mais do que o necessário para alcançar a compreensão, e o processo que resulta em distribuição aproximadamente igual de esforço leva à distribuição de quase-Zipfianas observada. Outra teoria fala que as estruturas linguísticas estão relacionados com modelos matemáticos de difusão ( que levam a uma distribuição semelhante.)

Em suma, essa lei é muito interessante, pois mesmo que não tenhamos nem um conhecimento agregado de outra línguagem, ainda teremos a capacidade de extrair informações com base na frequência de cada informação.

Descobrindo novas linguagens (universalidade?)

Imagine que um 🛸👽 mande uma mensagem para você com o seguinte conjunto de dados (supondo que o árabe não exista e que a quantidade de dados seja extremamente gigantesca):

[...]
مرحبا أيها الغريب. هذا نص عشوائي أرسله إليك حتى تتمكن من محاولة فهم لغتي. لهذا السبب ، سأرسل لك حوالي ثمانية مليارات بيانات. أتمنى لك الحظ الجيد
[...]

Fica a pergunta: Como você iria analisar essa quantidade de dados?

Neste momento, irei levantar duas hipóteses:

1ª Hipótese: A civilização dos 👽 é muito mais complexa e possui estruturas linguisticas mais abundantes e estruturadas.

Neste caso, talvez a abordagem de criamos uma espécie de dicionário com base na lei de zipf dos dados alienígenas falhe. Seria semelhante a um golfinho tentar entender a nossa linguagem. Mesmo com um arcabouço linguístico, nossas regras são complexas e a estruturação dos passos seria demasiadamente complexa para os golfinhos. Talvez poderíamos entender palavras e frases em um nível que os humanos suportem, mas não teríamos a capacidade de suportar uma complexa e intrincada comunicação. Entretanto, sob a ótica dos aliena, nossa linguagem seria simples e provavelmente não teriam muita dificuldade de entender as regras gramaticais.

2ª Hipótese: A civilização dos 👽 está em um nível tecnológico semelhante ao nosso e, portanto, as suas regras de comunicação não devem possuir uma diferença extremamente grande em relação a nossa.

Neste caso, talvez seja possível haver uma comunicação onde seríamos capazes de entender a estrutura linguística dos aliens! Juntando a lei de Zipf com algoritmos semelhantes ao do google tradutor, talvez a relação entre as duas estruturas seja feita.

Note que na hipótese 1 os aliens poderão nos entender e na hipótese 2, por sua vez, seria possível haver uma bidirecionalidade de informações. Assim sendo, seria a linguagem algo universal? Como comseguimos "matematizar" a nossa linguagem, seria possível falarmos que ela seria universal por provavelmente a matemática ser universal?

👋👋 Espero que tenham gostado dessa publicação. Comentem se possível e até a próxima! 😅😅

REFERÊNCIAS BIBLIOGRÁFICAS

[1] - Google Translate - Wikipedia. Disponível em: https://en.m.wikipedia.org/wiki/Google_Translate. Acesso em 4 de dezembro de 2022.

[2] - Google’s Neural Machine Translation System: Bridging the Gap
between Human and Machine Translation. Disponível em: https://arxiv.org/abs/1609.08144. Acesso em 4 de dezembro de 2022.

[3] - Tradução automática neural com atenção. Disponível em: https://www.tensorflow.org/text/tutorials/nmt_with_attention. Acesso em 5 de dezembro de 2022.

[4] - Zipf's Law - Wikipedia. Disponível em: https://en.m.wikipedia.org/wiki/Zipf%27s_law. Acesso em 5 de dezembro de 2022.