Algoritmo de busca binária - Binary Search
Neste post vou falar um pouco sobre o algoritmo de pesquisa binária, e como ele é muito poderoso em comparação com o algoritmo de pesquisa linear.
Resumidamente, o algoritmo de pesquisa binária é um algoritmo eficiente que divide a lista repetidamente pela metade até encontrar o item desejado. Seu funcionamento é determinado pela busca da metade, analisando se o valor da metade está muito longe ou perto do elemento que queremos encontrar.
Diferentemente da pesquisa simples ou pesquisa linear onde analisamos elementos por elementos em uma lista de array, o algoritmo de pesquisa binária é um algoritmo mais performático, levando menos tempo que o algoritmo de busca linear.
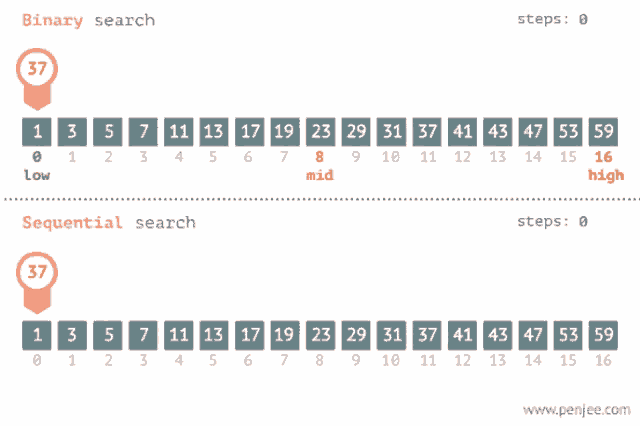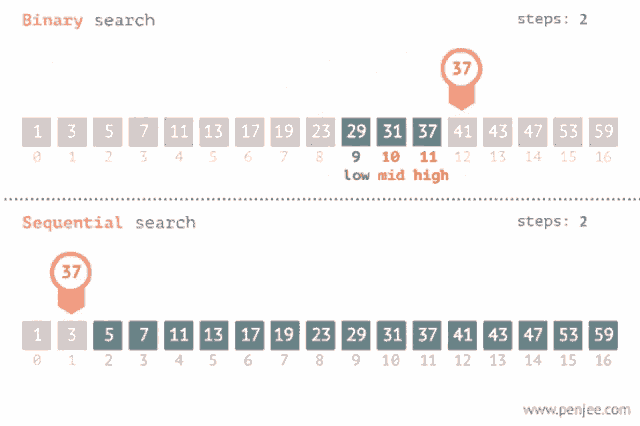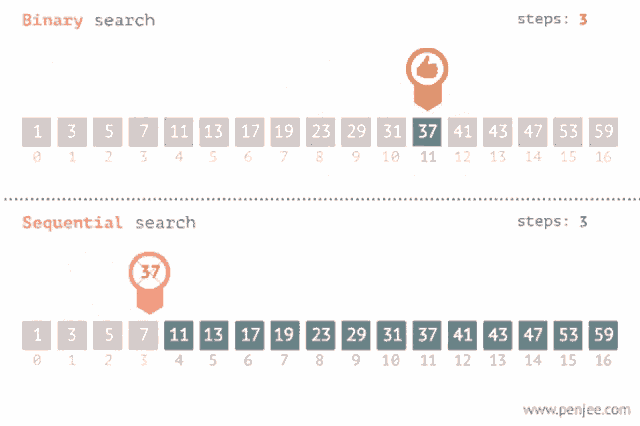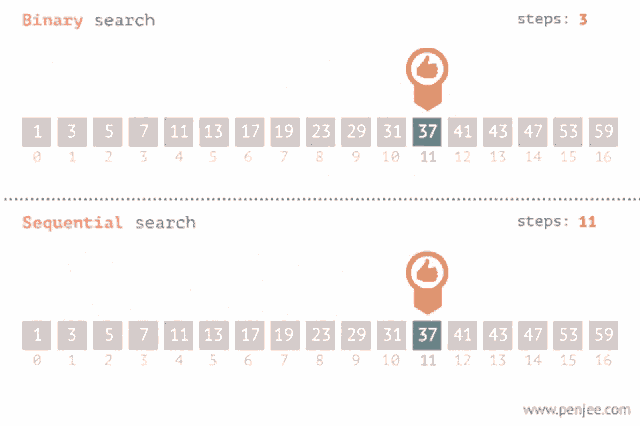
Como o algoritmo funciona na lógica?
Imagine o seguinte cenário. Voce deseja procurar em um dicionario a palavra "programação", como a palavra começa com a letra "p" você claramente iria iniciar a busca pela metade do dicionario, analisaria se a busca está muito proximo ou longe da letra que você está buscando e descartaria o restante, até chegar na letra "P".
Vejamos outro exemplo
Imagine que você tem uma lista de números de 1 a 100 e deseja encontrar o número 40 nessa lista. Você poderia percorrer essa lista analisando todos os elementos e verificar se o valor corresponde a 40. Mas esse tipo de algoritmo leva muito tempo para processar. Para resolver isso, vamos usar o algoritmo de pesquisa binária. Ele começará a pesquisa pela metade da lista, verificando se o valor desejado está muito próximo ou longe, eliminando assim os valores mais baixos e mais altos. Por exemplo, para encontrar o número 40, ele pode começar pela metade do array, que seria o número 50. Cinquenta está muito acima de 40. Portanto, ele pode eliminar os valores acima de cinquenta e analisar os valores abaixo de 50. Agora, imaginamos que o algoritmo chuta um número, digamos 30. Trinta é um valor abaixo de 40, então os valores abaixo de 30 não serão analisados. Logo, 40 está entre 30 e 50. Com isso, o algoritmo terá que buscar o número 40 entre 30 e 50, sempre dividindo a busca pela metade.
Funcionamento do Algoritmo
A função binarySearch vai procurar o item em um array ordenado. Se o valor que queiramos encontrar estiver no array sera retornado a sua posição, se o valor não estiver no array a função retornarar None.
- criando uma lista de 100 elementos de 1-100
listOfNumbers = list(range(1,101)) # [1,2,4,...,99,100]
Os elementos da lista devem está ordenado para que o algoritmo funcione. Se a lista tiver seus elementos desordenado, o algoritmo não vai funcionar.
- pegar o valor mais baixo e o valor mais alto
low = 0 # 0
high = len(listOfNumbers) - 1 # 99
- pegar o valor do meio e salvar na variavel o elemento do meio kick (chute)
middle = (low + high) / 2
kick = array[middle]
- analisar se o valor do chute corresponde ao item que queiramos encontrar.
if kick == item:
return middle
nessa parte, se o valor do chute for igual o valor do item que queremos encontra,será retornado sua posição.
- o chute for maior que o valor que queiramos encontrar, vamos atualizar o valor de
highpara uma nova posição.
if kick > item:
high = middle - 1
- O mesmo ocorre se o valor for menor que o valor que queremos encontrar.
if kick < item:
low = middle + 1
- se a função não encontrar o item na lista, a função ira retornar
None.
Código completo
listOfNumbers = list(range(1,101)) # [1,2,4,...,99,100]
# algoritmo de pesquisa binária
def binarySearch(array, item):
low = 0
high = len(array) - 1
while low <= high:
middle = int((high + low) / 2)
kick = array[middle]
if kick == item:
return middle
elif kick > item:
high = middle - 1
else:
low = middle + 1
return None
print(binarySearch(listOfNumbers, 40)) # retorno = 39
print(binarySearch(listOfNumbers, -40)) # retorno = None
Observe que, na busca do número 40, a função retorna sua posição 39. Se você analisar a lista, verá que o elemento da 39ª posição será exatamente o número 40.
Agora, observe que, na busca do elemento -40, a função retorna None, pois o elemento não existe na lista
algoritmo de pesquisa linear
listOfNumbers = list(range(1,101)) # [1,2,4,...,99,100]
def linearSearch(array, item):
for index in range(0, len(array)):
if array[index] == item:
return index
return None
print(linearSearch(arrayOfNumbers, 40)) # retorno = 39
print(linearSearch(arrayOfNumbers, -40))) # retorno = None
Comparando o número de operações usando Big O notation.
Em resumo, o que é Big O notation, é basicamente um meio de medimos a eficiencia de um algoritmo. Nesse post não me aprofundarei sobre o assunto, mas quem sabe em um post futuro.
No exemplo do algoritmo de pesquisa linear onde temos uma lista de 100 elementos, dizemos que o número de processos/tentativas é O(n) onde n é a quantidade de elementos na lista. Essa notação nos diz que o algoritmo vai precisar de 100 tentativas para encontrar o elemento que queremos. Se for uma lista de 4 bilhões de elentos, precisaria de 4 bilhões de tentantivas. Isso nos demonstra o quão demorado é esse método de pesquisa linear.
No caso da pesquisa binária a quantidade de tentativas que o algoritmo vai precisar vai ser bem diferente da quantidade de tentativa da pesquisa linear. O número de tentativa vai ser O(log2 n) onde n é a quantidade de elementos da lista. No caso da lista de 100 elementos, o número de tentativa que o algoritmos vai precissa é de 7 para poder encontrar o elemento.
❗Uma observação: A notação big O notation não é usada para medir o tempo de execulsão do algoritmo, mas a quantidade de operações que o algoritmo vai precissar. Através desse método podemos saber o quão eficiente é uma algoritmo.
conclusão
Neste post, aprendemos sobre um algoritmo superpoderoso e como aplicá-lo na prática, além de compará-lo com o algoritmo de pesquisa linear. Este post teve uma referência do livro Entendendo Algoritmos: Um Guia Ilustrado Para Programadores e Outros Curiosos, no qual estou me baseando. Qualquer dúvida, sinta-se à vontade para comentar; responderei com o maior prazer. Agora é a sua vez de implementar esse algoritmo. Deixe aqui nos comentários a sua versão. Vou gostar muito de ver o seu código.